Physicist: Black holes and space are both black, so there’s that. But while black holes tend to be very small, space is bonkers big and filled with just enough stuff to give astronomers things to look at while simultaneously getting in the way of looking at said things.
The now-famous actual picture of M87* taken in the microwave spectrum.
The picture that you’ve already seen is of M87*, the supermassive black hole (SMB) in the middle of the galaxy M87. Damn near every galaxy appears to have a SMB in its core. This isn’t a coincidence, they’re instrumental in the formation of galaxies. A galaxy’s SMB is almost always dead center and generally has a mass proportionate to the mass of the galaxy it calls home (or more likely, calls “mine”). Our home galaxy’s supermassive black hole, Sagittarius A*, has the mass of around 4.1 million Suns, which is pretty massive. But M87* weighs in at around 6.5 billion Suns, more than a thousand times bigger. M87* is massive even by supermassive standards.
Sagittarius A* is by far the closest SMB (a mere 26,000 light-years away), but of course there’s a galaxy in the way. To see it we have to look long-ways through the disk of the Milky Way, which is full of stuff. M87* on the other hand is a freaking monster, but it’s 54 million light-years away. That’s fairly nearby in galactic terms (you can see it on a dark night), but that’s still incomprehensibly distant. The light collected to create the picture of M87* was released when our branch on the tree of life was a bunch of tiny, arguably adorable critters, barely recognizable as primates, and expanding across a planet with a recent and notable lack of dinosaurs. In balance, it was easier to image M87*, a black hole a thousand times bigger and two thousand times farther away, than Sagittarius A*.
As a quick aside, that stunningly boring name, “M87”, comes from Messier (being French, his name is pronounced “mess-E-ay”). At the time astronomers were getting famous putting their names on comets (worked for Halley) and Messier wanted a part of the action. It turns out that to an 18th century telescope, there are lots of vague, blurry things in the sky that might be comets, but aren’t. So Messier wrote a list of things he didn’t want to look at twice, and that rejection list is what he’s remembered for now (incidentally, he also discovered some comets). The galaxy M87 is the 87th thing on Messier’s “ignore this” list.
Left: The disk of our galaxy (as viewed from inside our galaxy) obscures a band of the sky all the way around us, including the galactic core (home of Sagittarius A*). Right: As a super giant galaxy, M87 is visible to the naked eye from 54 million light years away. But as an elliptical galaxy, it looks like a smudge on the lens. That tiny blue tail is a jet of plasma (one of two) that’s been streaming out of the disk of gas falling into M87* for at least 5000 years.
The blurry doughnut is a cloud of in-falling gases that heat up and ionize as they fall in. M87*, despite being substantially larger than the orbit of Neptune, is much smaller than the cloud of stuff falling into it, so there’s a bottle neck as gas falls in and that means friction and compression and that means heat. That glow is a fire storm in space far bigger than our solar system. The dark in the middle isn’t the black hole itself, so much as a lack of gases. Newton’s gravity is proportional to the inverse square of the distance to whatever’s making the gravity; half the distance = four times the gravity, a third the distance = nine times the gravity. In Newton’s gravity, there’s no limit to how close you can be in orbit around something. But in Einstein’s (correct) formulation of gravity, the inverse square law is only an approximation that works in low gravity situations (basically, Newton is good enough for practically every application except black holes). It turns out that black holes have an innermost stable orbit, that’s 3 times the Schwarzchild radius (3 times the black hole’s radius). Anything that tries to orbit closer will just spiral in. The edge of that doughnut is the innermost stable orbit; the last chance gases have to glow before they get fast-tracked to the black hole itself.
The gas is about the same temperature all the way around M87*, but because it’s spiraling in it’s moving toward us on one side and away on the other. The side that’s moving toward us appears brighter because of an (usually difficult to notice) effect called “relativistic beaming“; very high speed material emits more light in the direction of motion (although, from its own perspective, it’s still emitting light evenly in every direction).
We were almost guaranteed to see that hot cloud of gas all the way around M87* because, in addition to all the other craziness going on, black holes bend light around them. This isn’t unique to black holes, we see “gravitational lensing” every time light passes close to something massive. In fact, one of the earliest confirmations of General Relativity was during the 1919 solar eclipse when stars were seen around the Sun that were actually behind it. So black holes aren’t the only things that can bend light beams, but they do elevate the art; instead of light being slightly deflected, it can completely change direction or even literally go into orbit. So when you see a stream of hot gas beside a black hole, it might actually be behind it. Regardless of how the disk of infalling hot gases are arranged, there will always appear to be gas around the black hole.
Gravitational lensing doesn’t just fun-house-mirror and confuse the image, it actually helps us here. The dark spot is three times the size of the black hole in reality (the innermost stable orbit), but the lensing effect magnifies it an makes it appear larger.
The gravity of the “red blob” galaxy in the foreground, LRG 3-757, bends the light a galaxy behind it so much that it appears as a ring. Gravitational lensing like this allows us to measure the distribution of mass by looking at how it warps the image of distant objects, and is sometimes even used intentionally (as a lens!) to get a better view of said distant objects.
The curse of always being right, I’ve been told, is that you’re never surprised and rarely invited to parties. The new black hole picture isn’t really a discovery, but it is a stunning accomplishment. Black holes, as we understand them today, were first theorized when Schwarzschild got ahold of the recently published equations of Einstein’s general theory of relativity, applied them to a dense sphere of matter, and followed where they led. Modern physics has an established track record of starting with basic assumptions, building verifiable theories, and then applying those theories to reach conclusions that everyone agrees are so completely nuts they can’t possibly be true. Black holes, which are real, are a great example of “so weird they can’t possibly be real”.
Today, you’d have a hard time finding an astronomer or astrophysicist who didn’t already firmly believe in the existence of black holes and their basic, overall properties. They quibble about the details, sure, but that’s scientists. There’s a long catalog of observations that already fell in line perfectly with the predicted nature of black holes. LIGO’s ongoing detections of gravitational waves are beautifully and precisely described by black holes merging. Stars in the galactic core get whipped back and forth at around 1% the speed of light (which is absurdly fast for anything that isn’t a particle) while orbiting a dark, compact “radio source”. Quasars, some of the brightest, highest energy things in the universe, are exquisitely described by gases falling into SMBs, but are totally mysterious otherwise.
So what did astronomers expect to see when they finally got a direct image of an actual black hole? Basically what we’ve seen. The simulations used to predict what a real picture would look like were disappointingly accurate.
A (non-blurry) image generated by a black hole simulation.
It would have been great if the picture had been completely different. Like a smiley face or something. Science advances when we’re wrong or surprised or both. What this new picture does is add another verification win to the theory of General Relativity, which is good. It’s not enough to have a clever theory that always works, you also have to give it every possible new opportunity to fail.
So as far as theory goes, we haven’t gained too much. This was kind of the “eat your vegetables” of empirical physics. What we gained, we gained through the effort it took to get this picture. The reason this hasn’t be done before is that it’s really, really hard to do. M87* is about 54 million light-years away and about 38 billion km across, which makes it 42 microarcseconds across. There are 360 degrees in a circle, 60 arcminutes in a degree, 60 arcseconds in an arcminute, and a million microarcseconds in an arcsecond. 42 microarcseconds is the angle across a single hair from 500 km away.
But here’s the problem: that’s too small. There’s a fundamental limit to the resolution of a telescope called the “diffraction limit” that’s built into the wave nature of light. The more perfectly your telescope is constructed, the closer you can get to this limit, but you can never do better. If D is the diameter of your telescope’s main lens or mirror and W is the wavelength of the light you’re using, then the smallest angle (in radians) you can resolve is about 
The Earth happens to be a few thousand km across, so we just need a way to use the whole thing. Enter the Event Horizon Telescope (EHT), an international collaboration of telescopes that points at M87* with an “effective aperture” that’s about the size of the Earth. A regular telescope creates images by collecting light and focusing it on a detector. A light wave from a distant source rolls in like a wall, bounces off of the mirror, and arrives at the focal point all at once. This is done automatically by the geometry if the mirror is parabolic, since every parallel path takes the same amount of time to get to the focus (that’s just one of those handy properties that parabolas have).
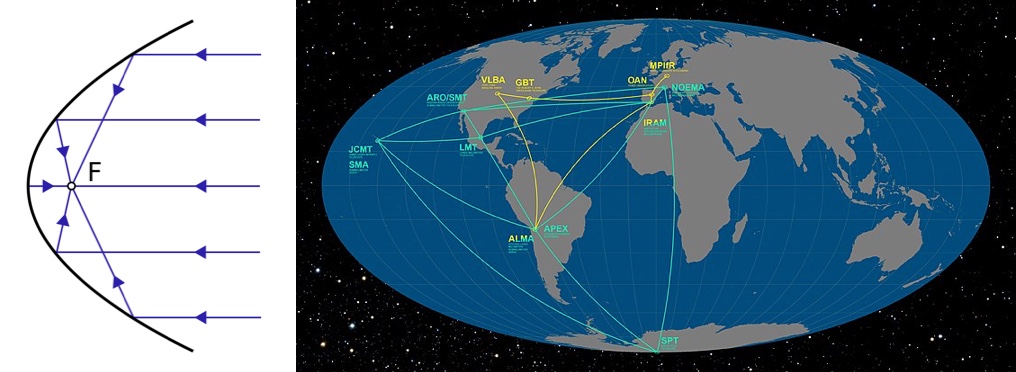
In order to function, a telescope bounces light waves so that they arrive at the detector all at once if they’re coming from the right direction. Left: In a regular telescope, the shape of the mirror does this automatically. Right: The Event Horizon Telescope has to put the wave back together using brute force; big computers and ridiculous precision.
If parts of the mirror happens to be missing, that’s fine. The wave still arrives at the focus all at once, but some of it just passes on through. So the fact that the EHT doesn’t need to cover an area the size of Earth, it just needs to have pieces spread out across the Earth. But there’s still a huge problem; the light waves rolling in from M87* are never collected at a focal point. Instead, the data received by each telescope and array is recorded, collected in a single location (often by loading hard drives onto a plane and physically bringing the data together), and processed using a technique called very-long baseline interferometry (VLBI). “Very-long baseline” refers to the fact that the distance between the individual telescopes is “very long”. “Interferometry” refers to the fact that the collected light waves need to interfere.
That interference is important; it’s not enough to just report what each telescope sees. Getting the wave front to arrive at the detector all at once is a really important part of what makes a telescope work. After all, waves from what you’re not looking at also arrive at your detector, just not all at once. Parts of the wave arriving at different times interfere destructively and cancel each other out. So there are two big hurdles: combining the data while also knowing exactly when a given light wave sweeping across Earth arrives at each different telescope’s detector. You need to be able to tell the difference between one wave front and the next, and if the next wave front is 1.3 mm behind and traveling at the speed of light, then you need to reliably distinguishing between events 4 picoseconds apart (4 trillionths of a second). So, every telescope needs a shiny new atomic clock and a really fast camera. You begin to get a sense of why the data consolidation looks more like a cargo shipment than an email attachment; trillions of snapshots every second of not just the waves you’re looking for, but also the waves that will cancel out once all the data is processed. Add to that the challenge of figuring out (generally after the fact) where every detector is to within a fraction of a millimeter even as their orientation changes and the Earth rotates, and you’ve got a problem.
Or had a problem anyway. The picture came out just fine. The two black holes that appear the largest from Earth are Sagittarius A* (because it’s close) and M87* (because it’s a monster), and they’re both right on the edge of what can be effectively imaged using Earth based arrays of telescopes like the EHT. But if the overarching history of technology is any indication, the first time is almost impossible and the thousandth is embarrassingly easy. We’ll get better pictures of M87* and passable pictures of Sagittarius A* soon. Once we set up an array of space telescopes throughout cislunar space (the volume inside the Moon’s orbit) we’ll get pictures of the SMBs in the cores of every nearby galaxy and that’s when the science really gets started. The cost low Earth orbit has dropped by 99% since 1980 and the price of spaceflight in general is on schedule to drop substantially more in the decades to come, so a fleet of space telescopes is not such a big ask.
That blurry picture of M87* is the first stumbling steps into a profound new kind of astronomical research that will be totally routine sooner than you think.
The Milky Way picture is from here.
The simulated black hole image is from here.
